计算化学

课程

University of Minnesota Chem 4021/8021 Computational Chemistry by Prof. Christopher J. Cramer: bilibili, YouTube, Essentials of Computational Chemistry: Theories and Models.

参考书

Solids and Surfaces: A Chemist’s View of Bonding in Extended Structures, 固体与表面.

基本概念

前线轨道理论

两个分子的轨道相互作用：1 和 2 稳定化、3 能量升高（反键 $\Delta E$ 上升 > 成键下降）、4 无直接能量效应（电子未占据）。

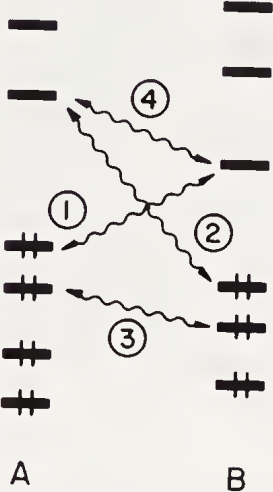
分子与固体表面作用：

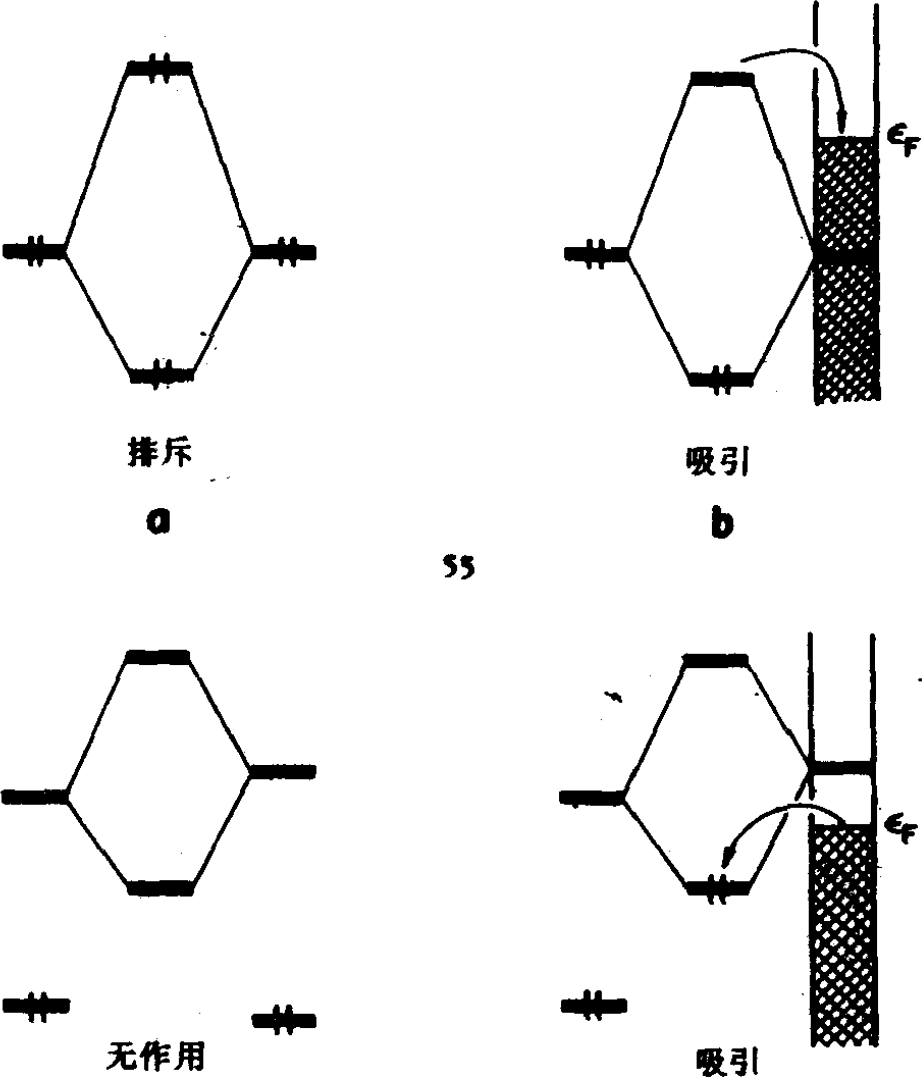
能带

原子离得越近，能带展宽约显著。

能带折叠

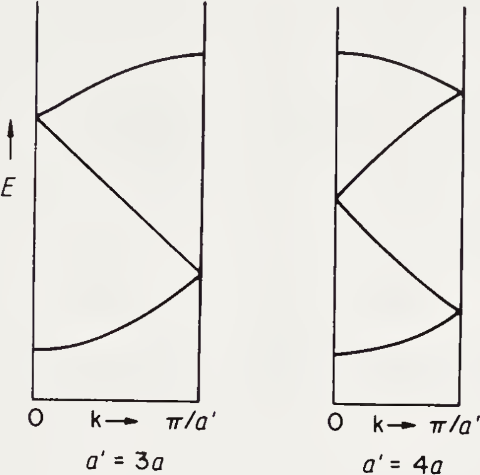
单胞扩大一倍相当于将原来的能带对折：

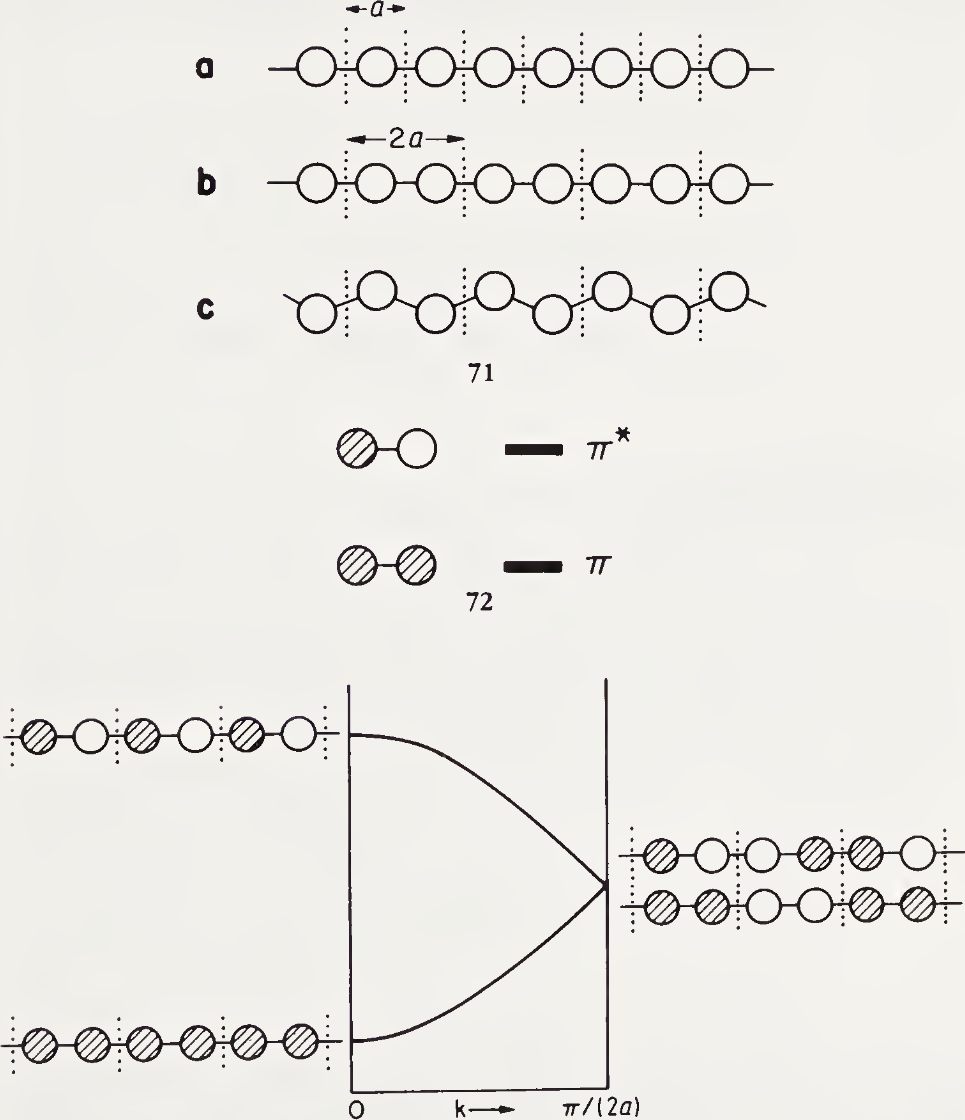
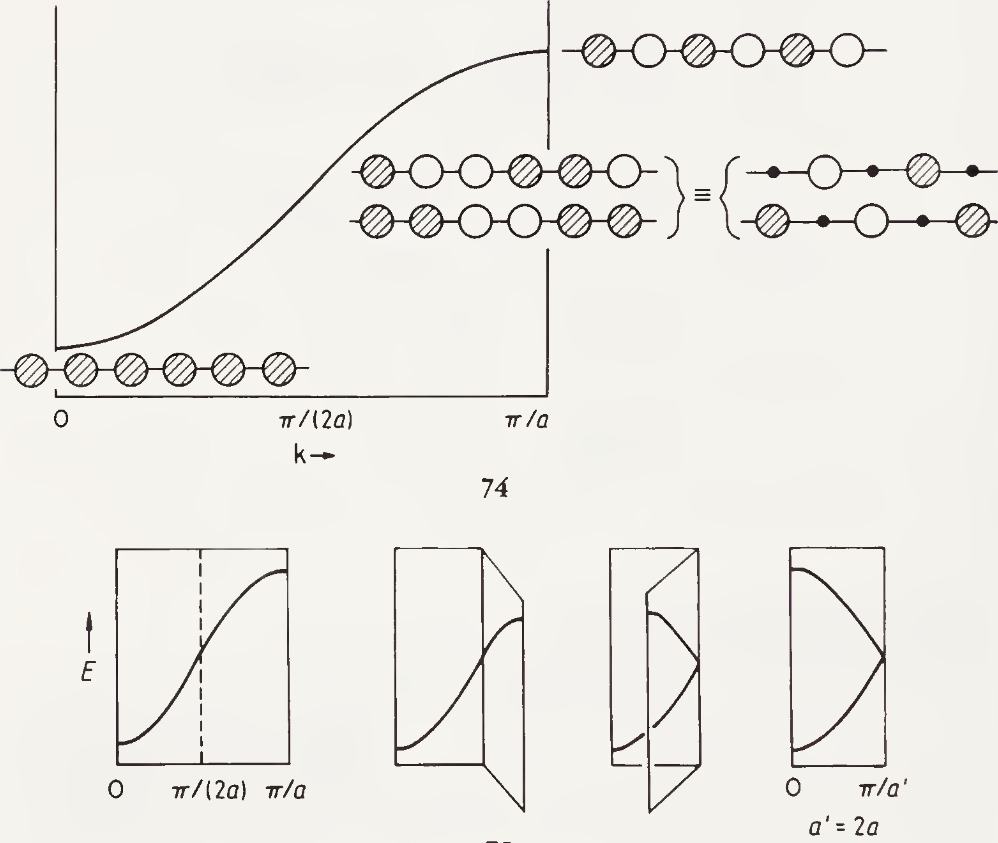
类似的，扩大两倍、三倍就相当于对折两次、三次。

DOS - Density of State 态密度

$\text{DOS}(E)\text{d}E$ = $E$ 与 $E+\text{d}E$ 之间的能级数

能带越平的地方 DOS 越大：

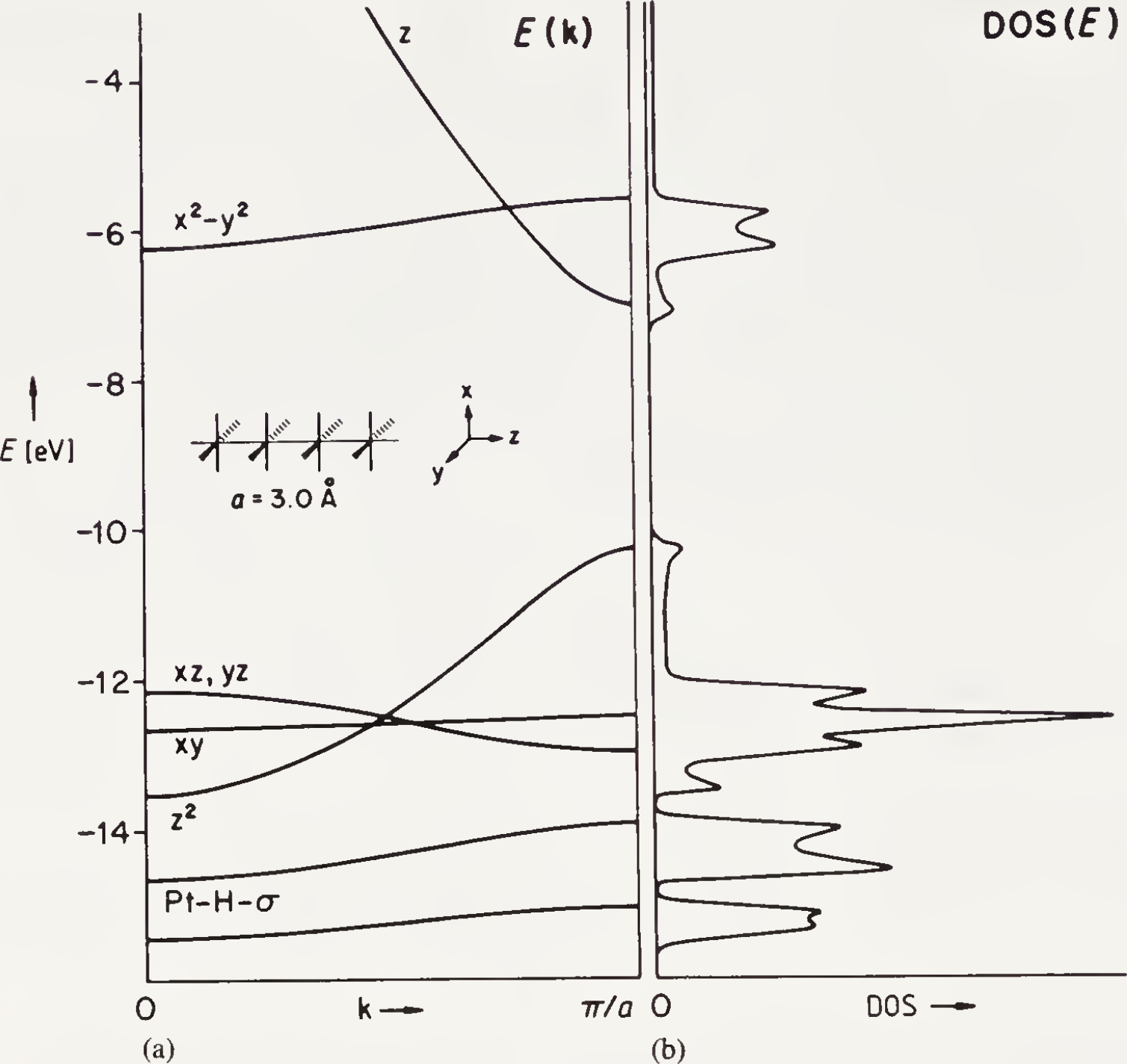
积分到费米能级再 ×2 就是电子总数。描绘电子按能量的分布。

PDOS

P = Projected: 分解特定原子轨道或者原子的贡献

把 Kohn-Sham eigenstates $\ket{\psi_{n}}$ 投影到一组相互正交的基函数上 $\bra{}$，一般是原子轨道。我们就能得到每个原子所分摊的 DOS，叫做 PDOS。

PDOS 可以用于研究在周期性体系中的局域环境下的电子结构，对于能带所属的原子轨道成分分析非常有用。

我们把体系中所有原子的 PDOS 叠加得到的就是总 DOS，在实际的分析过程中，我们经常要把不同元素和不同轨道分开分析，所以 PDOS 也是非常常用的。

COOP - Crystal Orbital Overlap Population 晶体轨道重叠布居

即重叠布居权重的 DOS (overlap population-weighted density of states)。

双中心分子轨道 $\Psi=c_1\chi_1+c_2\chi_2$ 有 $1=\int|\Psi^2|\text{d}\tau=\int|c_1\chi_1+c_2\chi_2|^2\text{d}\tau=c_1^2+c_2^2+2c_1c_2S_{12}$, $S_{12}$ 是 $\chi_{1}$、$\chi_{2}$ 间的重叠积分。$c_i^2$ 表示分配到中心 $i$ 上的部分，$2c_1c_2S_{12}$ 称为重叠布居。重叠布居值的正负（成键、反键）取决于 $c_{1}$ 和 $c_{2}$ 同异号。

N₂:

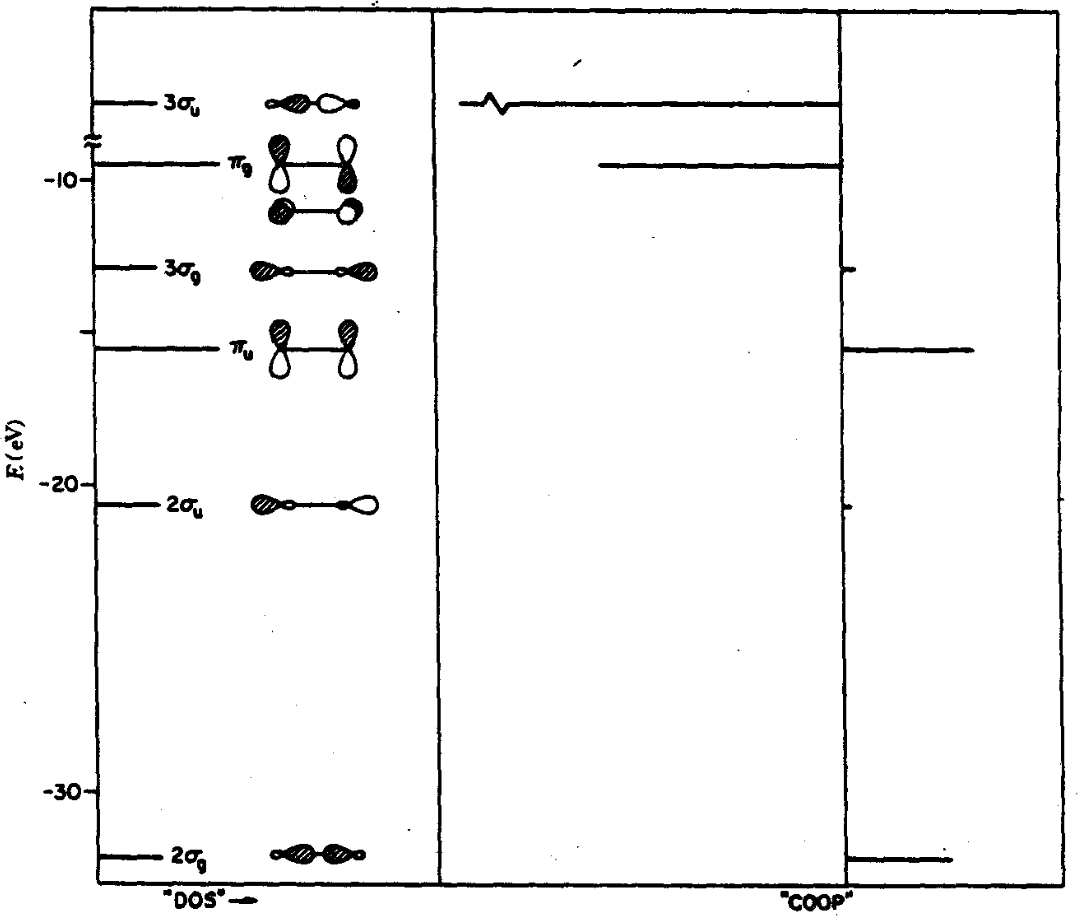
COOP 曲线在正的区域成键，负的区域反键，0 附近非键。

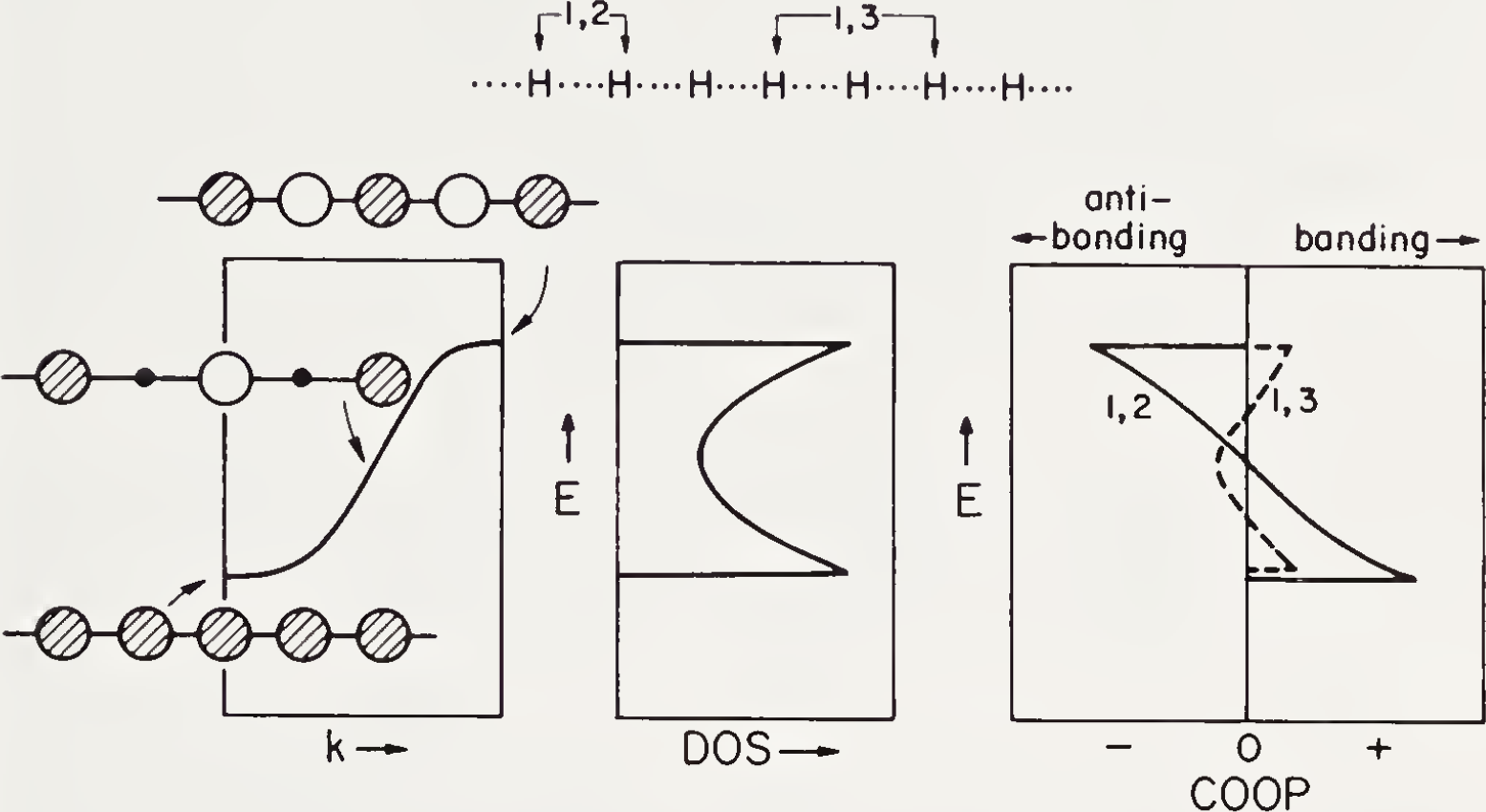
COOP 曲线积分到费米能级为该键的总重叠布居。DOS 和 COOP 为晶体中电子占有情况和键级指数的微分表示。

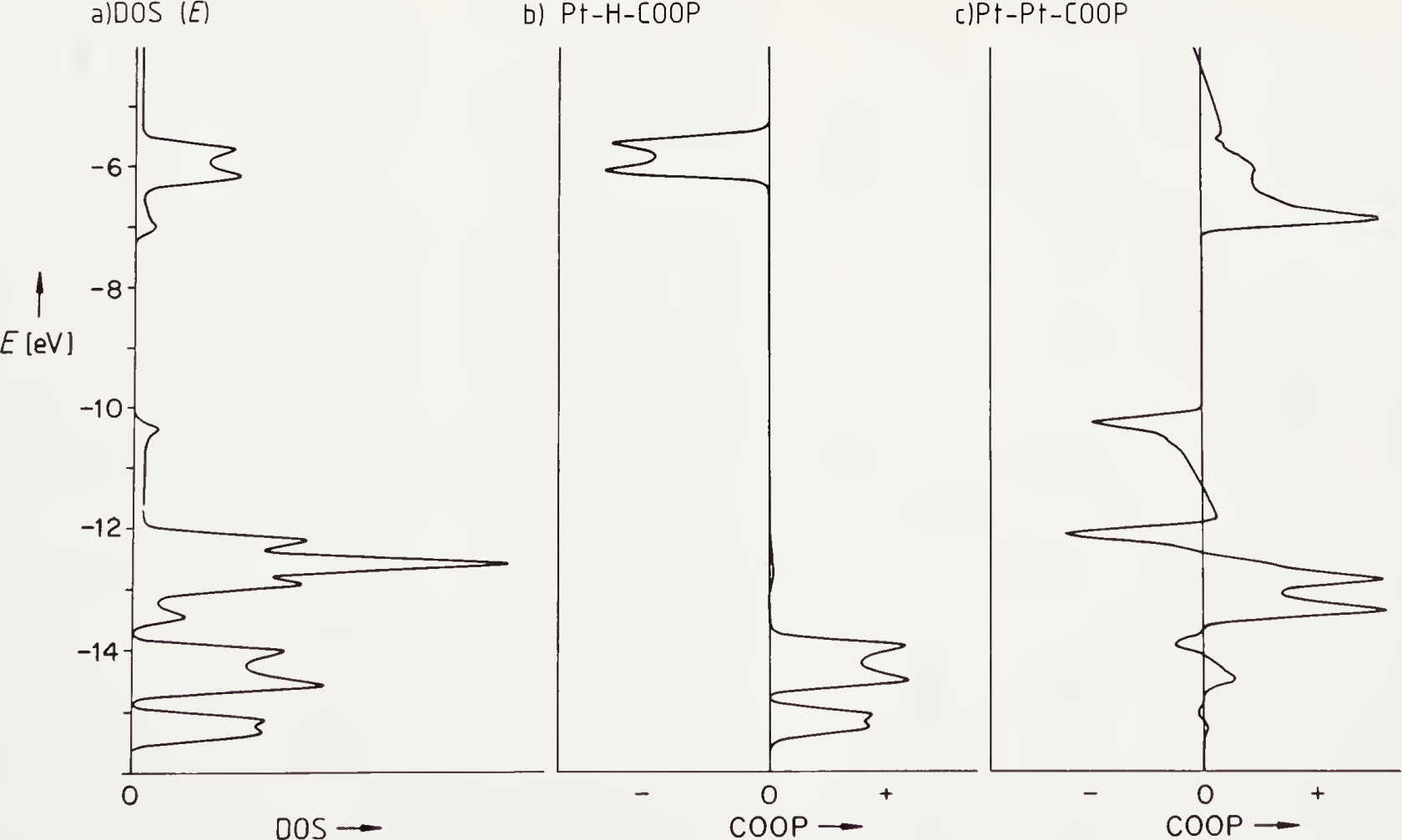
其中对 -10~-13 eV 部分 Pt-Pt-COOP 的解释：

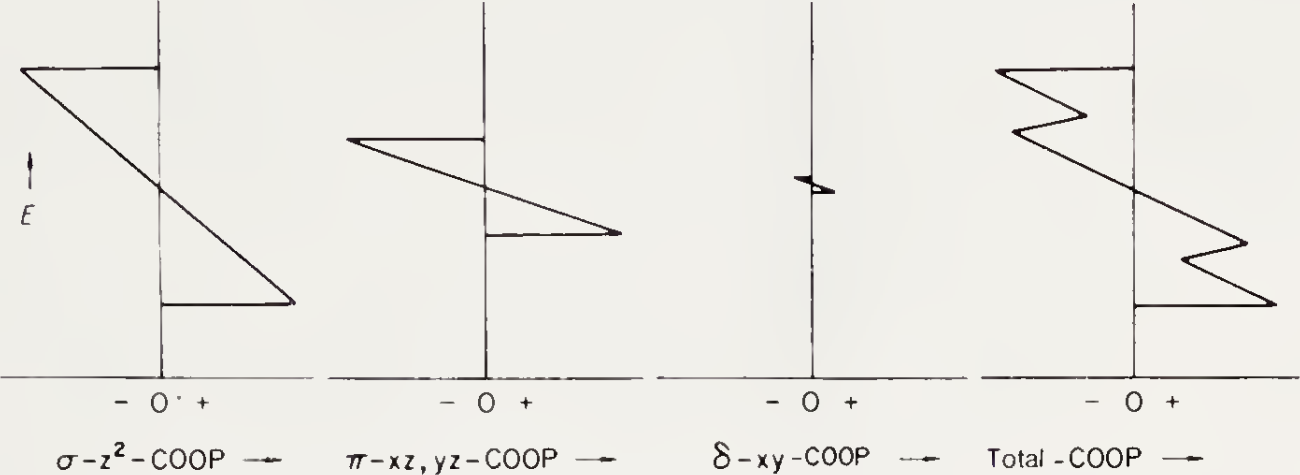
COHP : Crystal Orbital Hamilton Population

COOP 中的重叠布居矩阵用哈密顿矩阵代替。